De Morgan’s Laws are the most important rules of Set Theory and Boolean Algebra. This post will discuss in detail about what are De Morgan’s Laws, details about first law and second Law, verification of these laws and their applications.

What are De Morgan’s Laws

Augustus De Morgan was a British Mathematician who formulated laws or rules of Set Theory and Boolean Algebra that relates three basic ‘Set’ operations; Union, Intersection and Complement. De Morgan laws are a couple of theorems that are related to each other.

In Propositional Logic and Boolean Algebra, these laws are seen as rules of transformation. These laws can be proved using Venn Diagrams and Truth-tables.

Fig. 1 – Introduction to De Morgan’s Laws

De Morgan’s texts were outstanding which included Algebra, Trigonometry, Differential and Integral Calculus, Probability and Symbolic Logic. De Morgan pioneered Propositional Calculus. He devised Algorithm for approximating factorials in the 19th Century.

Fig. 2 – Augustus De Morgan

De Morgan’s Laws

The two laws stated by him are:

• De Morgan’s Law of Union or First Law
• De Morgan’s Law of Intersection or Second Law

De Morgan’s Law of Union or First Law

The first law or the Law of Union states that: If A and B are two finite sets or subsets of a Universal Subset U then, the element not in A ∪ B is not in A’ and not in B’. Conversely, it also states that an element not in A’ and not in B’ is not in A ∪ B. i.e.

(A U B)’ = A’ ∩ B’ where:

∪ denotes the Union (OR).

A’ refers to the set complement (NOT) of A in U, i.e., A’ = U\A

It can also be defined as; the complement of the union of two sets is the same as the Intersection of their complements; i.e.

Not (A or B) = Not A and Not B

De Morgan’s Law of Intersection or Second Law

The second law or the Law of Intersection states that an element not in A ∩ B is not in A’ or not in B’. Conversely, it also states that an element not in A’ or not in B’ is not in A ∩ B. i.e.

(A ∩ B) ‘ = A’ ∪ B’ where:

∩ denotes the Intersection.

It can also be defined as; the complement of the Intersection of two sets is the same as the Union of their complements; i.e.

Not (A and B) = Not A or Not B

Fig. 3, shows Venn Diagram representing logical relations between finite sets.

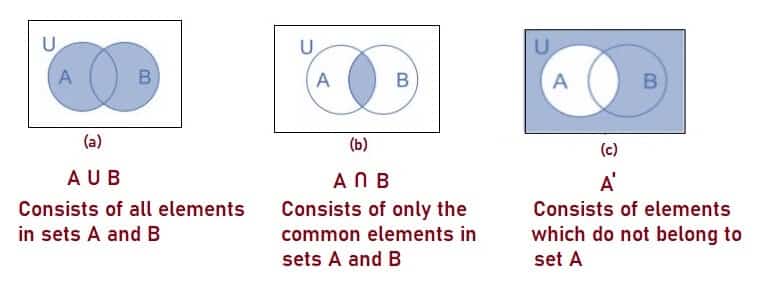
Fig. 3 – Venn Diagram of Finite Sets

Verification of First and Second Law

The laws can be verified or proved as shown below:

Verification of De Morgan’s Law of Union or First Law

 (A U B)’ = A’ ∩ B’

Let P = (A U B)’ and Q = A’ ∩ B’

Let x be an arbitrary element of P then x ∈ P ⇒ x ∈ (A U B)’

⇒ x ∉ (A U B)

⇒ x ∉ A and x ∉ B

⇒ x ∈ A’ and x ∈ B’

⇒ x ∈ A’ ∩ B’

⇒ x ∈ Q

Therefore, P ⊂ Q ……………. (i)

Again, let y be an arbitrary element of Q then y ∈ Q ⇒ y ∈ A’ ∩ B’

⇒ y ∈ A’ and y ∈ B’

⇒ y ∉ A and y ∉ B

⇒ y ∉ (A U B)

⇒ y ∈ (A U B)’

⇒ y ∈ P

Therefore, Q ⊂ P …………….. (ii)

Now combine (i) and (ii) we get; P = Q i.e. (A U B)’ = A’ ∩ B’. Hence proved.

Example of De Morgan’s Law of Union or First Law 

Let us consider two finite sets ‘P’ and ‘Q’ in the universal set U and

Let U = {1, 2, 3, 4, 5, 6, 7, 8}, P = {4, 5, 6} and Q = {5, 6, 8}.

Now let us verify: (P ∪ Q)’ = P’ ∩ Q’.

P ∪ Q = {4, 5, 6} ∪ {5, 6, 8}

= {4, 5, 6, 8}

Therefore, (P ∪ Q)’ = {1, 2, 3, 7}   ……………….. (i)

As we know P = {4, 5, 6} so, P’ = {1, 2, 3, 7, 8}

and Q = {5, 6, 8} so, Q’ = {1, 2, 3, 4, 7}

P’ ∩ Q’ = {1, 2, 3, 7, 8} ∩ {1, 2, 3, 4, 7}

Therefore, P’ ∩ Q’ = {1, 2, 3, 7}   ……………….. (ii)

Combining (i) and (ii) we get;

(P ∪ Q)’ = P’ ∩ Q’. Hence proved.

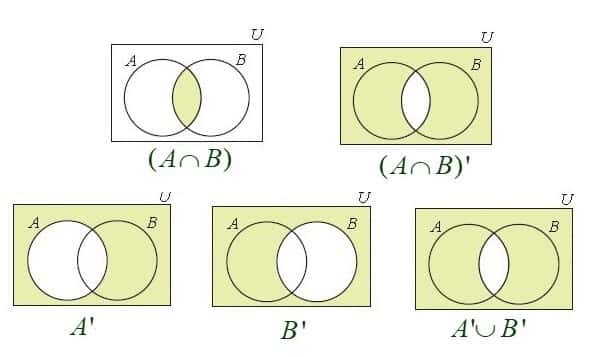
Fig. 4 – Venn Diagrams Representing De Morgan’s Laws

Verification of De Morgan’s Law of Intersection or Second Law

(A ∩ B)’ = A’ U B’

Let M = (A ∩ B)’ and N = A’ U B’

Let x be an arbitrary element of M then x ∈ M ⇒ x ∈ (A ∩ B)’

⇒ x ∉ (A ∩ B)

⇒ x ∉ A or x ∉ B

⇒ x ∈ A’ or x ∈ B’

⇒ x ∈ A’ U B’

⇒ x ∈ N

Therefore, M ⊂ N ……………. (i)

Again, let y be an arbitrary element of N then y ∈ N ⇒ y ∈ A’ U B’

⇒ y ∈ A’ or y ∈ B’

⇒ y ∉ A or y ∉ B

⇒ y ∉ (A ∩ B)

⇒ y ∈ (A ∩ B)’

⇒ y ∈ M

Therefore, N ⊂ M ……………. (ii)

Now combine (i) and (ii) we get; M = N i.e. (A ∩ B)’ = A’ U B’. Hence proved.

Example for De Morgan’s Law of Intersection or Second Law

If U = {j, k, l, m, n}, X = {j, k, m} and Y = {k, m, n}.

Now let us verify: (X ∩ Y)’ = X’ U Y’.

We know, U = {j, k, l, m, n}

X = {j, k, m}

Y = {k, m, n}

(X ∩ Y) = {j, k, m} ∩ {k, m, n}

= {k, m}

Therefore, (X ∩ Y)’ = {j, l, n} ………………. (i)

Again, X = {j, k, m} so, X’ = {l, n}

and Y = {k, m, n} so, Y’ = {j, l}

X’ ∪ Y’ = {l, n} ∪ {j, l}

Therefore, X’ ∪ Y’ = {j, l, n} ………………. (ii)

Combining (i)and (ii) we get;

(X ∩ Y)’ = X’ U Y’. Hence proved.

Applications of De Morgan’s Laws

These two laws are of utmost importance in various branches of mathematics and engineering.  We have seen how they can be applied in mathematics.  Similarly, they are applied both in computer and electrical engineering.

These laws are used in designing digital circuits and in verification of SAS code. These laws can also be applied in text searching by using AND, OR and NOT, collectively known as Boolean Operators.

Think of a set containing the words cats and dogs. According to De Morgan’s Laws:

Search A:  NOT (cats OR dogs)

Search B: (NOT cats) AND (NOT dogs)

Limitation of De Morgan’s Laws

The laws relate conjunction and inclusive dis-junction through Negation.

Also Read:
Ohms Law – Voltage, Current & Resistance Relation, When Not Applicable
Kirchhoff’s Laws of Current & Voltage – Application, Advantage, Limitation
Electromagnetic Induction – Theory, Application, Advantage, Disadvantage